アートビスケットデザインスクールへ ようこそ！
フィボナッチ数列とは、自然界や宇宙に見られる規則性のある美しい数列のことです。この数列をグラフにすると、世界で最も美しいとされる螺旋が描かれ、黄金比と呼ばれるデザインに欠かせない形状になります。このページでは、フィボナッチ数列とデザインとの関係をわかりやすく解説しています。フィボナッチ数列一覧を参照し、アートやデザイン制作にぜひお役立てください。
フィボナッチ数列とデザインには、数学的な美しさと自然なバランスが関係しています。フィボナッチ数列とは、前の2つの数を足して次の数が決まる数列です。たとえば、0, 1, 1, 2, 3, 5, 8, 13, 21...というように続きます。この数列には多くのデザインや自然界に見られる「黄金比」と関連があります。
フィボナッチ数列の数が大きくなるにつれて、隣り合う数字の比率は約1.618に近づきます。この比率は「黄金比」として知られ、建築や芸術、デザインの分野で調和や美の象徴とされています。黄金比を取り入れることで、人々にとって自然でバランスの取れたデザインとして認識されることが多いのです。
デザインにおいて、フィボナッチ数列を用いてレイアウトを決定することがあります。たとえば、ウェブデザインやポスター、雑誌のレイアウトにフィボナッチ数列に基づくグリッドを採用すると、要素の配置に自然な視覚的バランスが生まれます。
フィボナッチ数列は自然界にしばしば見られます。例えば、花の中心に見られる螺旋や貝殻の形などがこの数列に従っています。この数列をデザインに取り入れることで、自然界の美しさを反映したデザインを創り出すことができます。
フィボナッチ数列に基づく「フィボナッチスパイラル」は、貝殻や銀河など自然界の形状を模倣しています。このスパイラルは、建築やロゴデザインなどに取り入れられ、視覚的な動きとダイナミズムを生み出します。
デザインにおいて、フィボナッチ数列を取り入れることで、自然で心地よいバランスと美しさを表現することが可能になります。
フィボナッチ数が自然界において顕著に見られる植物
カラーリリー
カラーリリー（アクアホワイト）に見られる1枚の花びらのように見えるものは、花の根元につく1枚の葉「苞（ほう）」で、これは美しくても花びらではありません。その役割は花を保護したり、際立たせるための役割を持つ特別な葉なのです。
四葉のクローバー
幸せを呼ぶことで有名な四葉のクローバーですが、実はクローバーは遺伝子で3枚と決まっています。しかし、クローバーが成長中に踏まれるなどして、葉のもととなる原基に傷がつくことで葉が増えるというのが四葉になった原因のようです。
ラナンキュラス
ラナンキュラスの花びらを数えてみましたが、種類により144枚より多かったり少なかったりで、144枚と一致しません。このように144枚以上の花びらの数は極めて少ないことから、この数「144枚」が自然界におけるフィボナッチ数の限界値だと考えられています。
原則、花びら0枚がイネ科と裸子植物、花びら3枚がユリ科、花びら4枚がアブラナ科、それ以外の植物は花びら5枚で、限界数は144枚と覚えましょう。
1枚や2枚の花びらしかない花は、自然界ではほとんど見られないようです。しかし、植物の奇形や特定の条件下でそのような花が見られることがあるそうです。
1枚や2枚の花びらは、これまで見たことがありません。あれば、その情報をどなたかお問い合わせページから教えていただけると嬉しいです。
| No. | 計算式 | フィボナッチ数 |
|---|---|---|
| 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, ∝ | ||
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 0 + 1 | 1 |
| 3 | 1 + 1 | 2 |
| 4 | 1 + 2 | 3 |
| 5 | 2 + 3 | 5 |
| 6 | 3 + 5 | 8 |
| 7 | 5 + 8 | 13 |
| 8 | 8 + 13 | 21 |
| 9 | 13 + 21 | 34 |
| 10 | 21 + 34 | 55 |
| 11 | 34 + 55 | 89 |
| 12 | 55 + 89 | 144 |
| 13 | 89 + 144 | 233 |
| 14 | 144 + 233 | 377 |
| 15 | 233 + 377 | 610 |
| 16 | 377 + 610 | 987 |
| 17 | 610 + 987 | 1597 |
| 18 | 987 + 1597 | 2584 |
| 19 | 1597 + 2584 | 4181 |
| 20 | 2584 + 4181 | 6765 |
| 21 | 4181 + 6765 | 10946 |
| 22 | 6765 + 10946 | 17711 |
| 23 | 10946 + 17711 | 28657 |
| 24 | 17711 + 28657 | 46368 |
| 25 | 28657 + 46368 | 75025 |
| 26 | 46368 + 75025 | 121393 |
| 27 | 75025 + 121393 | 196418 |
| 28 | 121393 + 196418 | 317811 |
| 29 | 196418 + 317811 | 514229 |
| 30 | 317811 + 514229 | 832040 |
| 31 | 514229 + 832040 | 1346269 |
| 32 | 832040 + 3524578 | 2178309 |
| 33 | 3524578 + 2178309 | 3524578 |
| 34 | 2178309 + 3524578 | 5702887 |
| 35 | 3524578 + 5702887 | 9227465 |
| 36 | 5702887 + 9227465 | 14930352 |
| 37 | 9227465 + 14930352 | 24157817 |
| 38 | 14930352 + 24157817 | 39088169 |
| 39 | 24157817 + 39088169 | 63245986 |
| 40 | 39088169 + 63245986 | 102334155 |
| 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, ∝ | ||
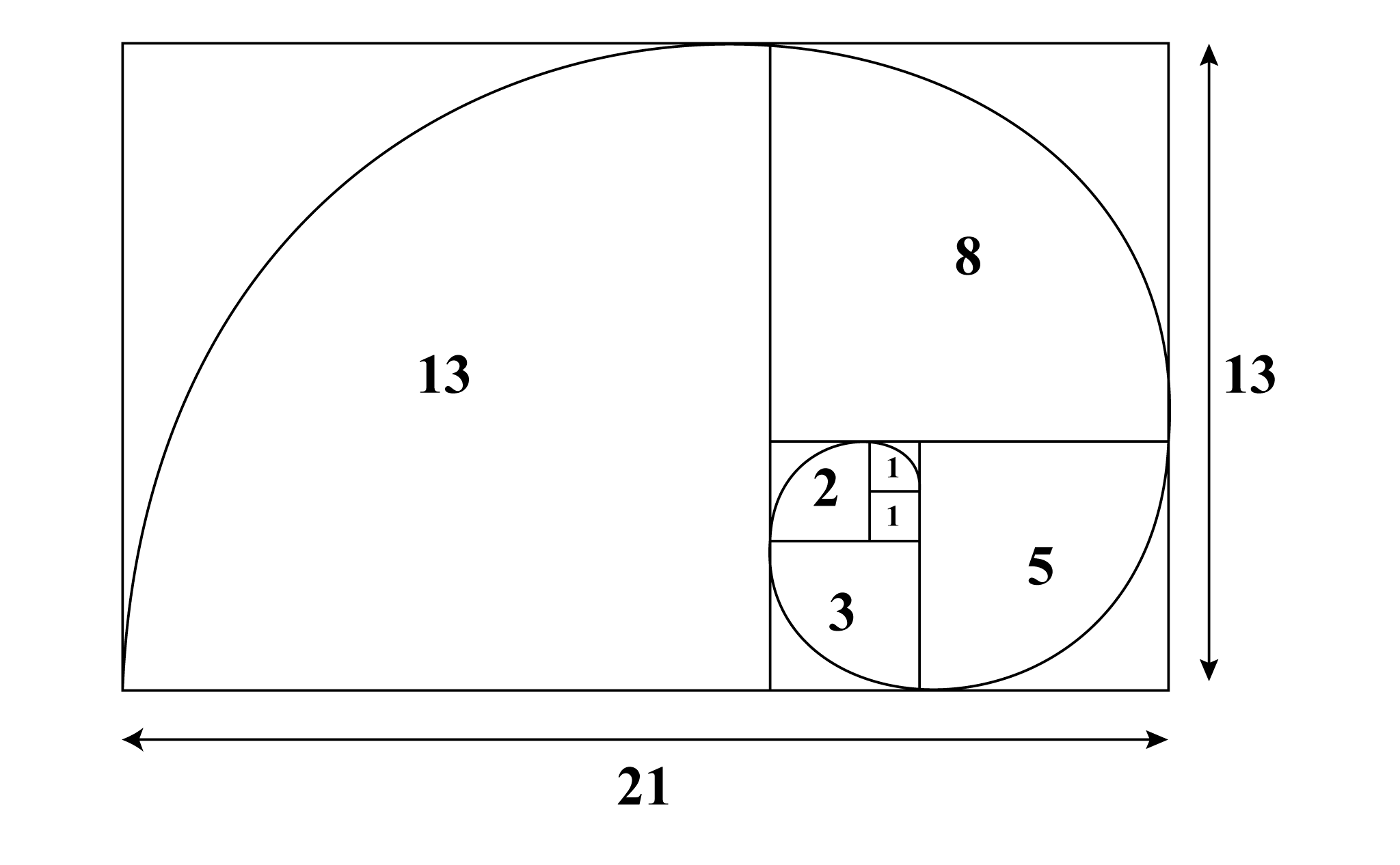
黄金螺旋
黄金長方形にあるすべての正方形の列において角の点を繋ぐと、渦巻き状の螺旋を描かれます。これが黄金螺旋です。
黄金螺旋の形状に似たものは、オウムガイの殻、ひまわりの種、台風の渦といった自然界に多く存在しており、大自然の造形美といえます。
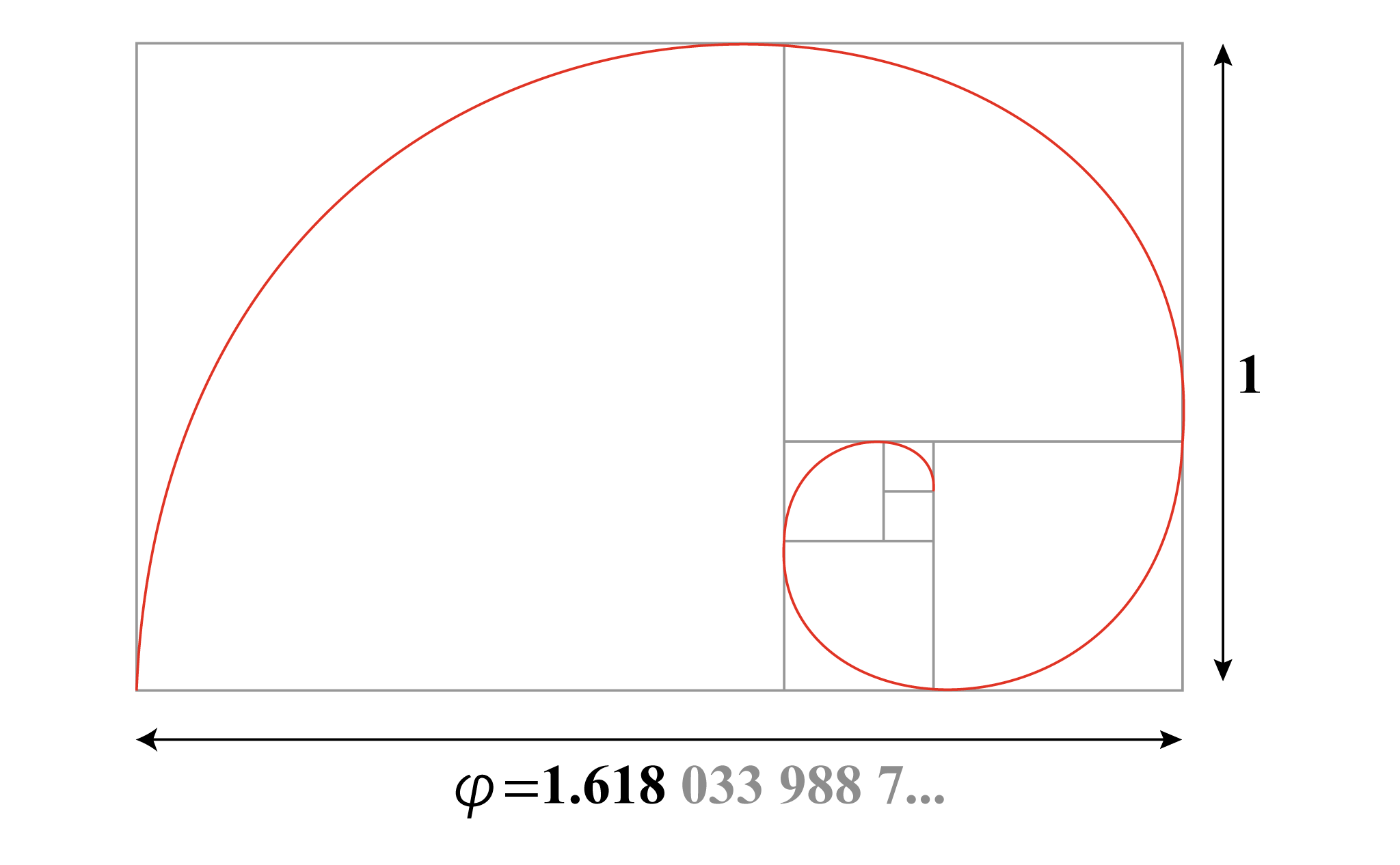
黄金長方形
縦と横の比率が「1:1.618」の比率となっているものを黄金長方形（黄金比）と呼ばれています。
正確な黄金比は、「1:1.618 033 988 7…」というように、円周率と同じように小数点以下が限りなく続きます。
下記画像3点の縦横比は、縦1・横1.618にしています。
オウムガイ
ひまわりの種
台風
フィボナッチ数列を用い表現したデジタルアートオブジェ。
写真に縦横の比率「1:1.618」の黄金長方形（黄金比）螺旋を乗せてみました。
フィボナッチ数列を用い表現したモノトーンのフォトアート。
